Ride share blowout sale
A certain ride sharing company sent me the following offer: pay $20 up front and your rides will be $4.50 ($2.50 for the carpool version) for 28 days. Is this a good deal? Let’s find out!
My immediate reaction was positive but then I had the feeling I was being duped. The key is to remember that the rides still cost money after the deal. So if my typical ride was $14.50, I don’t save $9 after only two rides ($29 - $20), I just break even because I still paid $9 for the rides. I’m guessing this sort of reasoning is intuitive, and why they might offer the deal.
However, there are certainly conditions where this is a good deal, so that’s what I’ll explore here. Basically, we just need to calculate how many rides one needs to break even. There are two important pieces of information needed to answer this question:
- The minimum fare per ride to set our minimum average: $5.45 for regular and $5.60 for carpool (as of writing this).
- Average true cost per ride: we’ll look over a range of values.
This problem can be solved using algebra. Essentially, we want to know when the true cost of rides will exceed the reduced cost plus the premium fee. There are two variables here, average true cost be per ride (C) and total rides (T):
\[C*T > 20 + T * 4.50\]We just need to solve for T (note that C > 4.5 because our minimum fare):
\[T > \frac{20}{C - 4.50}\]Now to do in R.
library(tidyverse)
theme_set(theme_bw() + theme(legend.position = "top"))
reduce_fare = data_frame(
service = c("Regular", "Carpool"),
reduce_fare = c(4.5, 2.5)
)
average_fare_data = crossing( #like grid.extra
service = c("Regular", "Carpool"),
average_fares = seq(5.45, 25, by = 0.01)
) %>%
left_join(reduce_fare, by = "service") %>%
mutate(
optimal_ride = ceiling(20/(average_fares - reduce_fare)) # ceil since we can't take partial rides
)
ggplot(data = average_fare_data, aes(x = average_fares, y = optimal_ride, colour = service)) +
geom_line(size = 1.5) +
scale_y_continuous("Rides to break even", breaks = seq(0, 20, by = 2)) +
scale_x_continuous("Average true fare", labels = scales::dollar) +
annotate("point", x = 12, y = 2, size = 2.5, shape = 3, stroke = 2) + # my information
annotate("label", x= 12, y = 1.25, label = "My usage", size = 8) +
scale_color_discrete("") +
theme(
text = element_text(size = 26),
axis.title = element_text(size = 32),
legend.position = c(0.9,0.9),
legend.justification = c(1,1)
)
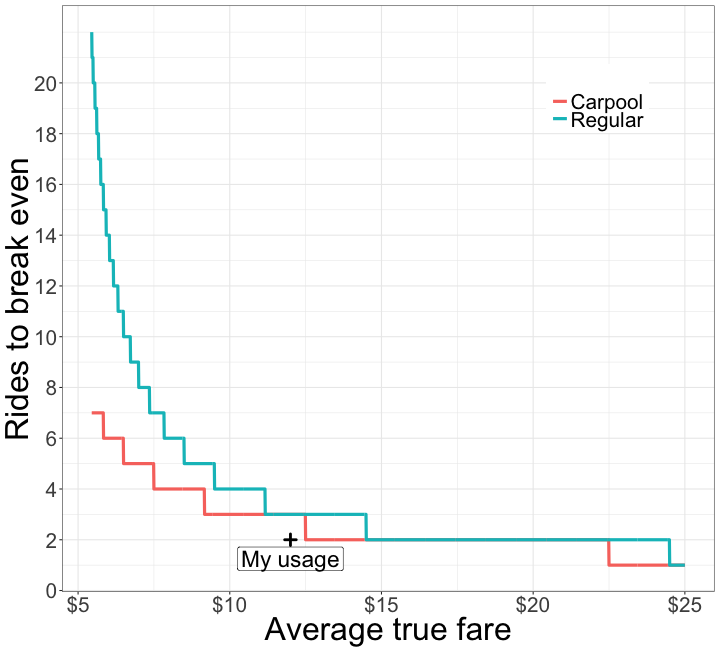
Basically, this is a good deal for frequent riders who already spend a lot on the service, and better for carpool users. It is also good for someone who knows they have upcomong multiple fares > $15 and any fare $25 or greater. One additional thing to consider, while you may break even, your actual savings won’t be too high if your typical rides are inexpensive. If you are riding at minimum fare, it takes 20 rides to break even, and then you are making about a $1 per ride after. So it is actually “most lucrative” for expensive rides. There is a cap though, which I talk about below. Based on my personal average usage in the last three months (plotted), this deal is not worth it to me. Makes one wonder if usage statistics factor into customer selection for the offer.
Three issues I didn’t mention. First: tipping. If you tip (and you should!), and you are incentivized to take extra rides, this could cost you more money. Second is geographic limitations, which in this case means no airport ride deals. Third issue is the cap: the deal goes up to $25 but you pay the difference after reaching it. However, the break-even point (M) for a single ride is less than $25:
\[M*1 - [20 + 4.50*1] = 0\] \[M = 24.50\]Because of the cap and the $20 premium, the most you can save from one use of the deal is $0.50. So the main way the cap affects the deal is in the actual amount saved, specifically for an infrequent rider. Consider that if you average a true $25 per ride for 2 rides, your reduced paid fare could be as low as $9 (two $25 true fares, $21 saved!) or as high as $28.51 (a minimum $5.49 and a $44.51 true fare, only $1.49 saved). While the deal is technically worth it either way, your savings are a lot higher in the former case! For frequent riders, this discrepancy is less of an issue.